


Next: Über dieses Dokument ...
Up: Generalisierte Berechnungen in Iterativen
Previous: Hierarchiesätze
In Kapitel 6 werden alternierende iterative Arrays als Verallgemeinerung der
nichtdeterministischen iterativen Arrays eingeführt. Es wird gezeigt, daß
sich die meisten Aussagen (Abschlußeigenschaften, Hierarchiesätze, usw.)
über nichtdeterministische iterative Arrays auf alternierende iterative
Arrays übertragen lassen.
Ein zentraler Punkt ist dabei Lemma 6.6, in dem eine Normalform für
alternierende iterative Arrays hergeleitet wird. (Mir ist keine
entsprechende Aussage für andere Maschinenmodelle bekannt.) Mit diesem
Lemma lassen sich die Ergebnisse aus Kapitel 3 auf alternierende iterative
Arrays übertragen (Lemma 6.7 bis 6.11). Allerdings sind die Beweise
technisch aufwendiger. Da die meisten Beweise aus den Kapiteln 4 und 5 nur
die Hilfmittel aus Kapitel 3 benutzen, übertragen sich nun die
Ergebnisse auf alternierende iterative Arrays.
Besonders interessant sind:
- Es gibt auch eine Hierarchie über die Anzahl der alternierenden
Schritte (Korollar 6.13).
- Man kann keinen Nichtdeterminismus einsparen, indem man Alternierungen
zuläßt (Satz 6.12).
- Im Gegensatz zu nichtdeterministischen iterativen Arrays sind
alternierende iterative Arrays abgeschlossen unter Komplementbildung (Lemma
6.14). Also sind alternierende iterative Arrays echt mächtiger als
nichtdeterministische iterative Arrays (Satz 6.15). Die entsprechende Frage
für Turing-Maschinen ist noch ungeklärt. (Man weiß zum Beispiel nicht,
ob bei polynominialer Zeitbeschränkung nichtdeterministische
Turing-
Maschinen weniger mächtig sind als solche mit einer
Alternierung; d.h.
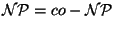 ?)
?)



Next: Über dieses Dokument ...
Up: Generalisierte Berechnungen in Iterativen
Previous: Hierarchiesätze
Andreas Klein
2000-01-11